卓球の試合における流れの可視化

テニスの試合の流れを可視化したく、確率シミュレーションを用いて勝率の推移をプロットしてみました【2018ウィンブルドン錦織】 | DataTennis.NET
このブログを参考にさせて頂き、卓球バージョンを自分なりにやってみました。
それっぽいやつはできたかなと思います。実際にやってみると、下のようなグラフになります。

2018年　全日本男子決勝　張本 9,5,-8,2,-6,5 水谷
オレンジ：張本選手　青：水谷選手

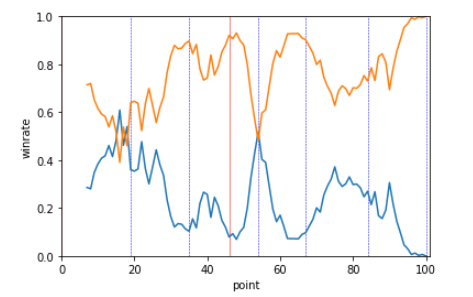
終始張本選手のペースなのがわかるかと。

2017年　世界卓球男子決勝　馬龍 -7,6,3,8,-5,-7,10 樊 振東
オレンジ：樊 振東選手　青：馬龍選手

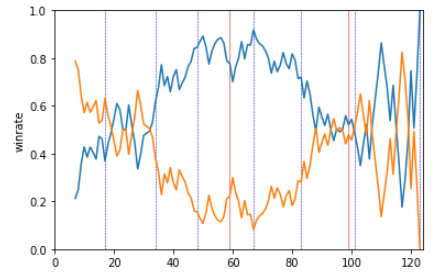
接戦だっただけに、最終セットまでわからない状況なのが見て取れる。

グラフの見方としては、

• 横軸　ポイント

• 縦軸　それぞれの選手の勝率

• 青線　セットの区切

• 赤線　タイムアウト

 となっていて、ポイントが進むにつれて、試合の後半になっていきます。

実際の試合をご覧いただくとわかると思いますが、それとなくは流れを可視化することができているんじゃないかと思います。セットを跨ぐ、タイムアウトが入ると流れも変わりやすくなっているのが感覚的にもしっくりきます。

今回のシミュレーションは直近の得点率から求めた確率に試合終了まで従うという非常に強引な得点計算方法であり、シミュレーターとしてはあまり優秀ではありません。実際の試合はお互いの心理状況、戦術などが複雑に絡み合い、その先の得点率に影響を与えているからです。

このあたりも考慮して後からどこでどんな流れだったのかを確認するのには使えるんじゃないかと思います。

20190905 追記 

ソースコードのインデントが崩れてしまい、修復できなくなったので、以下のファイルにまとめてあります。

colab.research.google.com

コード(python)は少し長いですがこんなんです。

import random
import matplotlib.pyplot as plt

両者の得点からシミュレーションに使う得点率を計算

def ratecalc(pla1Point,pla2Point):
 x = pla1Point / (pla1Point+pla2Point)
 return (x / 10) + 0.45

入力した状況（得点、セット数）から終わるまで試合を行う関数を定義。

def game_start(player1_point,player2_point,player1_setcount,player2_setcount,rate,game_match):
 #試合終了（どちらかが３セット先取）までループ処理
 while True:
 num = random.random()
 if num < rate:
 player1_point += 1
 elif num > rate:
 player2_point += 1
 #得点に応じて、セット終了かどうかを判定する
 if player1_point >= 11 or player2_point >= 11:
 #デュース判定、どっちがセットを取ったか判定
 if (player1_point - player2_point) ** 2 >= 4:
 if player1_point > player2_point:
 player1_setcount += 1
 else:
 player2_setcount += 1
 player1_point,player2_point = 0, 0
 if player1_setcount >= game_match:
 #試合終了,player1の勝利
 return 1
 if player2_setcount >= game_match:
 #試合終了,player2の勝利
 return 0
 return

gameStart関数を1000回ループして、勝率を計算する処理。

def game_roop(x1,x2,y1,y2,r,game_match):
 result = []
 for i in range(1000):
 result.append(game_start(x1,x2,y1,y2,r,game_match))
 return sum(result) / 1000

実際の試合の得点を入力し、gameroop関数をぶん回しながら試合終了まで行う処理。

def simulator(game_all,game_match=3,pla1_timeout = 0,pla2_timeout = 0,get_point_calc=8):
 player1_point, player2_point, player1_setcount, player2_setcount = 0, 0, 0, 0
 #セットごとの本数をカウント
 seq = []
 #得点率計算に使う本数-1
 get_point_calc -= 1
 pla1_winrate, pla2_winrate = [], []
 #配列から現在の得点とセット数を計算
 for i,point in enumerate(game_all):
 if point == 1:
 player1_point += 1
 else:
 player2_point += 1
 if player1_point >= 11 or player2_point >= 11:
 #デュースかどうか
 if (player1_point - player2_point) ** 2 >= 4:
 #どっちがセットを取ったか判定
 if player1_point > player2_point:
 player1_setcount += 1
 else:
 player2_setcount += 1
 player1_point,player2_point = 0, 0
 seq.append(i)
 if i >= get_point_calc:
 #getpointcalcで指定した本数で直近の得点本数を計算
 pla1_rate = sum(game_all[i-get_point_calc:i+1])
 pla2_rate = get_point_calc - pla1_rate
 #game_roop関数でシミュレーションする
 pla1_winrate.append(game_roop(player1_point,player2_point,player1_setcount,player2_setcount,ratecalc(pla1_rate, pla2_rate),game_match))
 pla2_winrate.append(1-pla1_winrate[-1])
 #グラフ描画用のコードを長々と記述
 p = plt.plot(range(get_point_calc,len(game_all)),pla1_winrate)
 p = plt.plot(range(get_point_calc,len(game_all)),pla2_winrate)
 p = plt.vlines(seq, 0, 1, linestyle='dashed', linewidth=0.5,colors='blue')
 p = plt.vlines(pla1_timeout, 0, 1, linewidth=0.5,colors='red')
 p = plt.vlines(pla2_timeout, 0, 1, linewidth=0.5,colors='red')
 p = plt.xlim(0, len(game_all))
 p = plt.ylim(0, 1)
 p = plt.xlabel('point')
 p = plt.ylabel('winrate')
 plt.show(p)

こんな感じで変数名の適当さなど突っ込みどころはあるでしょうけど、一応それっぽいやつはできました。
関数の定義が一通りできたので、動かしてみます。 

今回は水谷選手の得点時に1にする配列を用意して、これをsimulator関数に放り込むとグラフが出力されます。

#2018全日本男子決勝
mizutani_harimoto = [0,0,1,0,0,1,0,0,0,1,1,1,0,1,0,1,1,0,1,0,
                0,1,1,0,0,1,1,0,0,0,0,0,0,1,0,0,
                1,0,1,1,0,0,1,0,0,0,0,1,0,1,1,1,1,1,1,
                0,0,0,0,0,1,0,0,0,0,0,1,0,
                1,1,1,0,1,1,1,1,0,0,1,1,0,1,0,0,1,
                0,1,0,0,1,1,0,0,0,0,0,0,1,0,1,0]
simulator(mizutani_harimoto, 4, 46)

こっちも同様に。馬龍選手得点時に1となる配列。

#2017世界卓球男子決勝
maron_fan = [0,0,0,0,1,0,0,0,1,1,1,0,1,0,0,1,1,0,
                     1,1,1,1,0,0,1,1,0,0,0,1,1,0,1,1,1,
                     1,1,0,1,0,1,1,0,1,1,1,1,1,1,
                     1,1,0,0,1,1,1,1,0,0,0,0,1,1,1,0,1,0,1,
                     0,0,1,0,0,0,1,0,1,1,0,0,1,0,0,0,
                     0,1,0,0,0,1,0,0,1,0,0,0,1,1,1,0,1,0,
                     0,0,1,1,0,1,1,1,1,0,0,0,1,0,0,0,1,1,1,0,1,1]
simulator(maron_fan, 4, 59,99)

ちなみに、5セットマッチ、タイムアウトなしだと以下のように配列の入力だけで動きます。

simulator(array)

参考にさせて頂いたブログではサーブ時のポイント率から計算していますが、卓球の場合はテニスと異なりサーブは2本交代なので、サーブレシーブ関係なく、8ポイントで直近ポイントの得点率を求めています。4か8ポイントで求めるのがいいかなとは思いますが、7セットマッチということもあり、8ポイントで計算しています。

以上です。やってみたい人がいれば、動かしてみてください。